weak force and nuclear shells, revisited (II)

A -sort of- measurement of the Higgs Boson mass

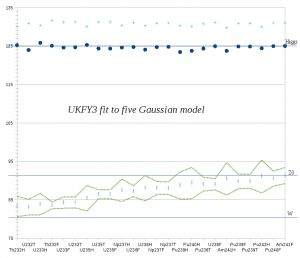
To put some numbers to our previous observations and go beyond eyeball line fit, we need to review the collections of nuclear fission data. There are two recent fits in the literature form which we can extract tables. The thesis of R.W. Mills “Fission product yield evaluation” (Birmingham, 1995), for the UKFY3 database, does a five-peaks fit of 24 (n,f) reactions, and we can pass to GeV the position of the asymmetric S1 channel and average all the reactions; this average is \(124.64 \pm 0.55\) GeV. Or we can use a more recent seven peaks fit, from D.M. Gorodisskiy, S.I. Mulgin, A.Ya. Rusanov, S.V. Zhdanov multi-modal analysis of (p,f) reactions (STI/PUB/1286, April 2008), and again look to the position of the S1 channel over ten different nuclides, getting an average of \(125.12 \pm 0.65\) GeV.

 

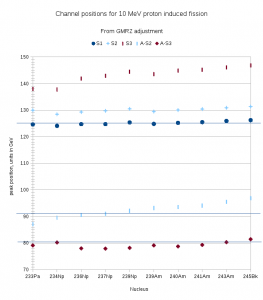
Channels in fission have been evaluated and systematized from the works of Wahl and, particularly, of Brosa, where one “standard symmetric” channel of equal-fragment fission and two “standard asymmetric” channels S1, S2 are considered. The latter are associated to peaks in the large fragment that in turn are linked so some shell closure or deformed shell closure.  More recently, the analysis of the external “wings” of the mass distributions has induced to add a third channel S3 associated to a peak in the small fragment; the GMRS analysis uses all the three channels plus a non-gaussian queue in the central, symmetric channel.

It comes without say that we do not still have a model of how or why should the electroweak bosons contribute to the nuclear potential in a way sensible enough to be part of the spin-orbit interaction that justifies the nuclear shells. Whatever it is, it should be a phenomena enhanced when the mass of the nucleus coincides with the mass of the electroweak boson, as we discussed ten years ago. By now, lets review the nuclear evaluations and we will come back in the next post to the question of the mechanism.

UKFY3 has been the evaluation eventually incorporated to the JEFF database . In the work of Mills it is considered that no better adjustment is got beyond five peaks -although the current evaluation seems to show an extra wing-,  and  then it makes visible the S1 and S2 channels of Brosa. They are supposed to be associated to the N=82 shell and to some other deformed neutron shell, and indeed the fit is nicely constant for the peaks in the large fragments.  Still, and given the absence of an electroweak particle of mass similar to the S2 peak,  for this channel we have painted in the graph, in light blue, both the large and small fragment peak. The position of the fragment is also undetermined by the average number of neutrons or light fragments that are emitted during the fragmentation, and so we have drawn bands around it.  We see in any case that, while increasing with the total atomic mass of the nuclei, this peak remains between the values of mass of the Z0 and W boson, and so I still hold to the conjecture is that S2 is really contributed by the lower fragment, that resonates with these bosons.

 

In fact this conjecture is partly supported by the GMRS analysis, who add to their fits a third channel S3 pivoting on the lower fragment.  In fact other groups have also considered that either the N=50 shell or the Z=40 and Z=50 shells should have some role in the “scission point” of the nucleus, so this addition is consistent. And the interesting point is that this S3 channel keeps constant very nearby of the mass of the W boson. The adjustment of the S2 channel improves in some sense too: while it is still best considered constant to a high-mass fragment, the average of the corresponding lower fragment, A-x (note that GMRS do not provide data on prompt neutrons), is pretty near of the mass of the \(Z^0\) boson. Without considering the noise from neutrons and light fragments, we had an average of \(92.34 \pm 2.91 \; GeV\) for the “A-x” S2 peak and \(79.21 \pm 1.14 \; GeV\) for the “A-x” S3.  Note that in the graphs the lines are set to the measured values of H, W and Z, not to these averages.

 

GMRZ 10 MeV protons

	S1	S2	S3	A-S2	A-S3
233Pa	124.6347	129.94425	137.95515	87.09525	79.08435
234Np	124.0758	128.45385	137.76885	89.51715	80.20215
236Np	124.72785	129.2922	141.86745	90.5418	77.96655
237Np	124.72785	129.75795	142.8921	91.00755	77.8734
239Np	125.3799	130.50315	144.47565	92.12535	78.15285
239Am	124.821	129.4785	143.54415	93.15	79.08435
240Am	125.1936	130.0374	144.84825	93.5226	78.71175
241Am	125.47305	130.41	145.22085	94.0815	79.27065
243Am	125.9388	130.87575	146.0592	95.47875	80.2953
245Bk	126.21825	131.3415	146.8044	96.876	81.4131
Averages	125.11908	130.009455	143.143605	92.339595	79.205445

Data from IAEA STI/PUB/1286 , table 4.5.5.

Converted with 1 AMU = 0.9315 GeV

UKFY3

Values in atomic mass units						Values in GeV
Â+ D1	 – D1	 + D2	2*Â	n	Reaction	 + D1	 – D1	 + D2	– D1 +n	– D1 +n
139.746	89.514	134.452	229.26	2.74	Th232H	130.173399	83.382291	125.242038	85.934601	80.642291
140.572	89.328	133.115	229.9	2.1	U232T	130.942818	83.209032	123.9966225	85.165182	81.109032
139.939	90.181	135.121	230.12	2.88	U233H	130.3531785	84.0036015	125.8652115	86.6863215	81.1236015
141.327	89.773	134.298	231.1	0.9	Th232F	131.6461005	83.6235495	125.098587	84.4618995	82.7235495
140.879	90.581	133.784	231.46	1.54	U233F	131.2287885	84.3762015	124.619796	85.8107115	82.8362015
140.943	90.597	133.876	231.54	1.46	U233T	131.2884045	84.3911055	124.705494	85.7510955	82.9311055
139.681	91.879	134.531	231.56	3.44	U235H	130.1128515	85.5852885	125.3156265	88.7896485	82.1452885
140.92	92.88	133.53	233.8	1.2	U235T	131.26698	86.51772	124.383195	87.63552	85.31772
140.92	92.88	133.529	233.8	1.2	U235F	131.26698	86.51772	124.3822635	87.63552	85.31772
139.93	94.07	133.8	234	3	Np237H	130.344795	87.626205	124.6347	90.420705	84.626205
140.766	93.754	133.958	234.52	1.48	U236F	131.123529	87.331851	124.781877	88.710471	85.851851
139.916	94.664	133.225	234.58	3.42	U238H	130.331754	88.179516	124.0990875	91.365246	84.759516
140.604	94.636	133.936	235.24	1.76	Np237F	130.972626	88.153434	124.761384	89.792874	86.393434
140.671	94.629	133.997	235.3	1.7	Np237T	131.0350365	88.1469135	124.8182055	89.7304635	86.4469135
139.926	95.414	132.538	235.34	3.66	Pu239H	130.341069	88.878141	123.459147	92.287431	85.218141
139.645	96.115	132.876	235.76	4.24	Pu240H	130.0793175	89.5311225	123.773994	93.4806825	85.2911225
140.414	95.726	133.535	236.14	1.86	Pu238T	130.795641	89.168769	124.3878525	90.901359	87.308769
140.823	95.677	134.173	236.5	1.5	U238F	131.1766245	89.1231255	124.9821495	90.5203755	87.6231255
139.354	97.286	132.871	236.64	4.36	Am241H	129.808251	90.621909	123.7693365	94.683249	86.261909
140.584	96.476	134.087	237.06	1.94	Pu239F	130.953996	89.867394	124.9020405	91.674504	87.927394
140.579	96.541	134.089	237.12	1.88	Pu239T	130.9493385	89.9279415	124.9039035	91.6791615	88.0479415
139.599	97.961	133.591	237.56	4.44	Pu242H	130.0364685	91.2506715	124.4400165	95.3865315	86.8106715
140.667	97.293	134.185	237.96	2.04	Pu240F	131.0313105	90.6284295	124.9933275	92.5286895	88.5884295
140.681	98.139	134.231	238.82	2.18	Am241F	131.0443515	91.4164785	125.0361765	93.4471485	89.2364785
					averages	130.762650375	87.560767125	124.639668	89.769974625	85.1891004583

From Â, D1, D2 values in Mills 1995
Value of n is A - 2*Â