A couple weeks ago, the account @iwontoffendyou twitted the following problem.
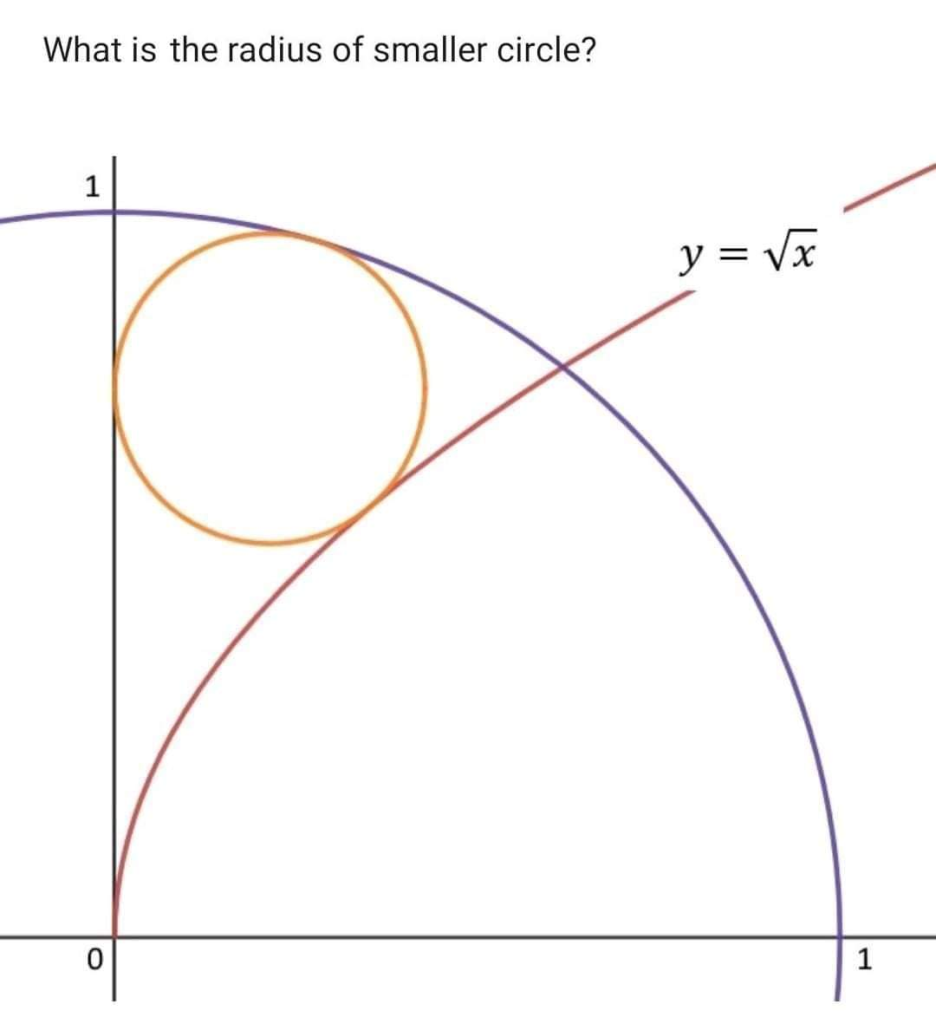
It was presented as a «round 1» exercise for employee interviews. So the logical path is first to try to answer either analytical or numerically, and only after a good enough answer is produced one can step back and look are more fun details.
Two observations are then evident:
That keeping the r=1 «perimetral» circle and the line fixed, the locus for the circles tangent both to line and perimetral is a parabola with focus in the origin and directrix x=1.
That the radius has been chosen such that it is the onset of multiple solutions for tangents. The circle with center in the horizontal axis is also solution, and for r > 1 it divides in two inner solutions, touching either the positive or the negative branches of the parabola.
Surely this particular choosing was done in order to simplify the algebraic approach, but it could be hoped that it also simplifies a constructive approach even if of «solid» type. Note that any intersection with a quadric already forbids the generalisation of a «plane» construction, even if it exists for particular values.
As a practice, I have collected a book of constructions in geogebra here.
Deja una respuesta