De rebote y gracias a mi adicción a twitter, veo que se me había pasado por alto la «lección perdida de Feynman«, pese a que se publicó en 1996 y pese a que recientemente el grupo de geometría y mecánica de mi departamento la había revisitado, https://arxiv.org/abs/1605.01204.
Lo interesante de la lección no es tanto -aunque pueda ser parte de una respusta- el uso de la hodografa en el espacio de velocidades sino el hecho de que Feynman se interesara la discretización de caminos que emplea Newton.
https://twitter.com/arivero/status/1753547162363826208/photo/1
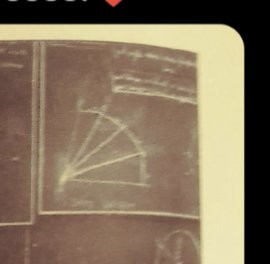
Este «Space Diagram» es, en mi opinión, el problema que retrasó años la publicación de los principia: Cómo probar la existencia de la curva clásica cuando necesitas probar que las áreas entre el camino discreto y la curva clásica tienden a cero en el límite continuo, y esas areas son esencialmente proporcionales a la cte de Planck. Pero eso ya lo he contado muchas veces, lo que veo interesante aquí es notar que al propio Feynman le interesó la cuestión… y que no debió de sacar nada en claro, puesto que no le valió para tirar hacia adelante en la cuestión de los fundamentos de la cuántica.
Y quizas por eso la gente no lo mira con tanta atención, porque tienen en el fondo el instinto de que si hubiera algo que rascar, los grandes ya lo habrían hecho.
En cualquier caso, en aquella época se formaria el Lore de que la integral de Feynman es una regularizacion de la delta de Dirac y que la probabilidad en cuántica debe ser compleja para que las soluciones clásicas interfieran entre sí de manera que las contribuciones de caminos con acción (¿o variación de la accion?) mucho mas grande que la cte de Planck se anulen, de forma que en el limite \hbar \to 0 se convierte la regularización en una autentica delta que selecciona el camino clasico. Eso era revolucionario en cuanto a fundamentos de la mecánica, y de la física.
Yo ataqué el problema un par de veces, en el año 98, primero con el grupoide tangente https://arxiv.org/abs/math/9802102 y luego con un intento de analyzar el peso de la integral de camino, https://a.rivero.nom.es/research/9803035.pdf. Por lo que veo ya se habia publicado la lección perdida, pero de alguna forma se nos escapó la relación.
Deja una respuesta