Carr’s duality

Carr’s duality is a series of attempts to work simultaneously with Compton wavelength of a mass M and the Schwarzschild distance associated to this same mass. So joining the domain of relativistic quantum mechanics with the one of black holes and general relativity.

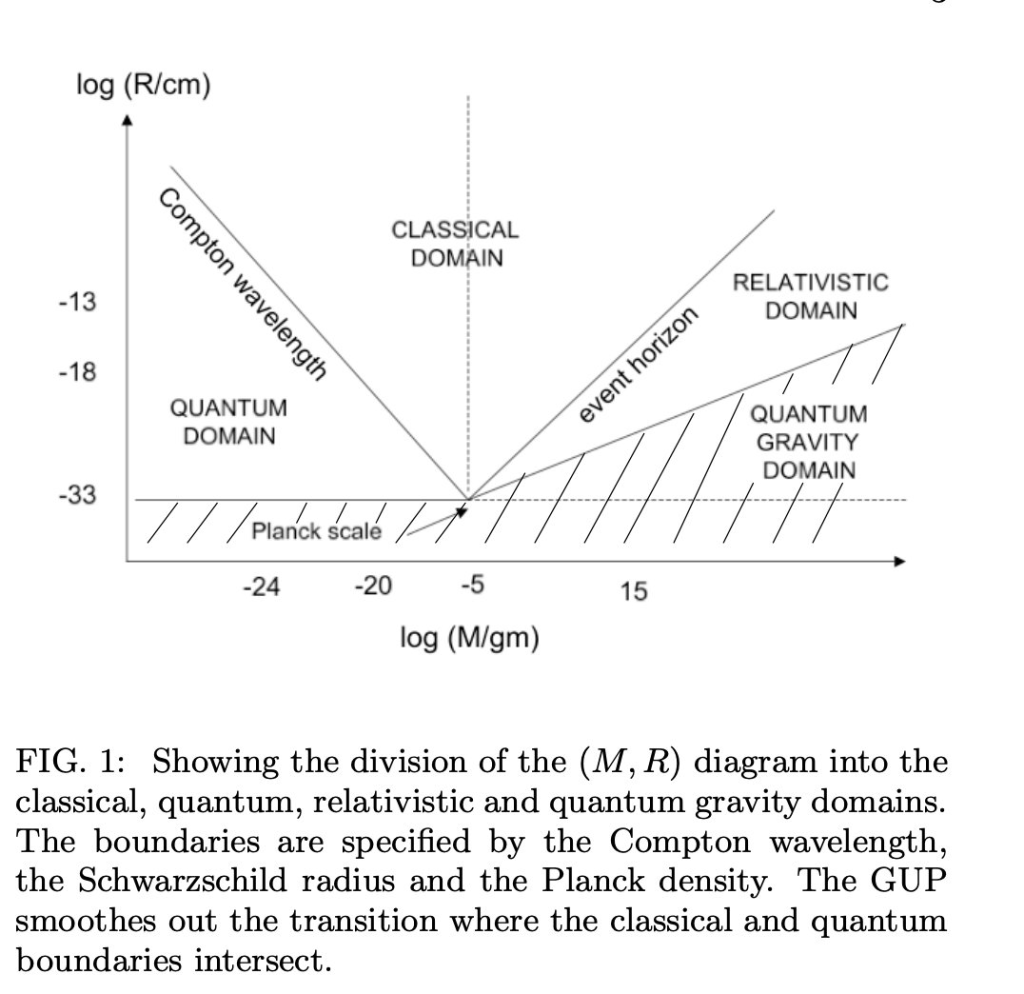
It has been referred in the literature as self-dual-blackholes, Black Hole Uncertainty Principle Correspondence, Compton-Schwarzschild duality and other names, usually associated with the unit of length from a Generalized Uncertainty Relation or Extended De Broglie relations.

To me, it seems related to the two conserved quantities of the classical Kepler problem: Energy and Angular momentum. We can pass from dynamics to kinematics dividing out by the mass of the test particle, and then these quantities become tangential speed and angular speed, at least when restricted to circular orbits (elliptical orbit is just a minor complication anyway). The classical theory domain is limited on one side when the tangential speed becomes the lightspeed c, for orbit radius of the order of the event horizon of the mass M, and on the other side when the areal speed becomes the Planck areal speed \(c L_P\), for radius of the order of the Compton wavelength of the mass M.

Of course, the «duality» is something as simple as seeing that the areal speed is \(\sqrt(G M r)\) and the tangential speed is \(\sqrt(G M / r)\). And as in some sense both QFT and GR are theories about distances, each limit is the door to one of them. I would not have been surprised if something similar had been found when Connes attempted to build a single Lagrangian for the standard model and general relativity.

It is also of some attraction to outsiders who find it independently; I am aware of twitter user Haug, who sees this as a way to build not-quantum experiments that measure Planck Length.

For other possible connections, see also in this blog https://a.rivero.nom.es/quantum-free-fall/ and https://a.rivero.nom.es/un-fundamento-de-la-mecanica-cuantica/, as well as https://www.physicsforums.com/threads/calculating-the-quantum-kepler-length-of-a-particle.14007/

EDIT: Addenda, note how any force is stronger than gravity, and then it means that for any other force as electromagnetism, the Planck areal speed is inside the Compton Length, and then non-existent due to fluctuations. Even before that, relativity starts to meddle with the tangential speed and then the angular momentum does not go to zero with the radius, but to a limit given by the coupling constant of the force.