Consideremos el modelo mas simple de voto prestado entre dos partidos: una bolsa de votos A, que vota unicamente a P, y una bolsa de votos C que por las razones que sea ha repartido su voto entre su partido tradicional, U, y la propuesta P.
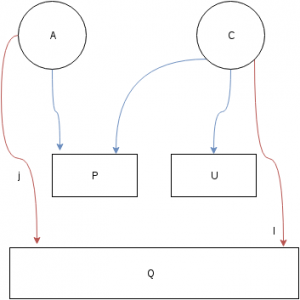
Ahora en la repeticion de las elecciones los dos partidos se unen formando la coalicion Q. ¿Podemos medir como reaccionan ambas bolsas de votantes? Pues no del todo. A fin de cuentas solo conocemos el resultado (P, U) y no el tamaño de los bolsos iniciales.
Si planteamos un modelo lineal, sabemos que A = P + U – C. Por tanto el nuevo voto
Q = j A + l C
lo podemos reescribir tambien como
Q = j (P + U – C) + l C = j P + j U + ( l-j) C
o como
Q = j A + l (P+U-A) = l P + l U + ( j-l) A
Y en ambos casos el coeficiente de P y el de U son iguales.
Ademas necesitamos al menos otra fuente de datos que nos permita eliminar una variable, C u A, y dejar todo como una expresion lineal de variables para las que tengamos alguna medida. Lo mas sencillo, si asumimos que C iba exclusivamente a U en elecciones pasadas, es buscar un sondeo o eleccion anterior, S, y asumir que el tamaño de C es proporcional a los datos de ese sondeo o eleccion anterior, digamos ?S. Con ello, bien aplicando C=?S en la primera formula, bien A=P+U-?S en la segunda, llegariamos a
Q = j P + j U + ?(l-j) S
y podemos intentar un ajuste lineal, usando la funcion LINEST() de Libreoffice u Excel. Claso esta, si el ajuste da coeficientes diferentes para P y para U, significa que alguna de las hipotesis de partida esta equivocada: o bien la eleccion del sondeo S, o bien la inicial del prestamo de votos desde una unica bolsa C; podria haber mas sensibilidades.
Por ejemplo, tomando como sondeo el porcentaje voto a IU en las elecciones del 2011, y P, U los porcentajes de votos a Podemos e IU en el 20D, un ajuste sobre treinta y cuatro provincias -las azules del post anterior mas canarias y cordoba- sugiere
Q = 0.77 P + 0.67 U + 0.19 S
con un error en estos coeficientes de 0.02,0.14 y 0.09 de manera que la diferencia entre los coeficientes de P y de U esta dentro del error, pero solo gracias a que este es bastante grande. Por otro lado si el modelo fuera admisible, tendriamos ?(l-j) = 0.19 > 0 y por tanto mayores perdidas porcentuales en la bolsa C que en la A, pero la diferencia real dependeria de cual es la relacion ? entre el sondeo S y el tamaño de C. Si asumimos que desde el 2011 la bolsa de IU habia crecido un factor 1.5, la diferencia seria 0.19/1.5. Y ademas hay que considerar tamaños absolutos: si las bolsas A y C eran muy diferentes, la perdida de votos puede ser mayor en porcentaje en C pero mayor en votos en A.
Esta cuestion del absoluto vs relativo nos recuerda que, ademas de la excesiva simplicidad del modelo, hay que tener en cuenta los efectos de peso que se producen al muestrear por provincias, de forma que en realidad acabamos dando mucho peso en el ajuste a regiones con menor poblacion. Sociologos habrá que de ello entenderán. Quizas convenga usar numero de votantes en vez de su porcentaje. Y por supuesto el modelo puede no ser el mismo en todo el territorio. En el ejemplo de arriba ya estamos usando solo provincias “no regionalistas” y que hayan tenido voto separado para IU y Pod en el 20D. Si ademas descartamos Canarias, que es tambien un outlier del post anterior, obtenemos
Q= (0.82± 0.03) P + (0.57± 0.14) U + (0.16± 0.08) S
Anunciando que algo va mal con la idea de las dos bolsas. Si ademas descartamos Cordoba, los coeficientes de P y U quedan definitivamente disparejos:
Q= (0.86± 0.03) P + (0.35± 0.14 U) + (0.20± 0.08) S
Aplicando la misma idea a las provincias con mayor porcentaje total de votos la situacion es diferente; recordad que estas no forman una nube sino una antidiagonal en el plano Pod/IU del 20D, pero cada una tuvo porcentajes de perdida muy dispares. En este caso lo que ocurre es que el coeficiente de P se acerca a 1 con un error bajo, pero el de U adquiere un error que lo hace inmedible, 0.77± 0.66, y similarmente el de S, -.34± 0.44. Con mucha fe podria considerarse que la antidiagonal si que admite el modelo de dos bolsas y es compatible, dado el signo negativo en el coeficiente de S, con una abstencion ligeramente mayor, en coeficiente, en la bolsa C, pero hay que ignorar unos errores de tamaño de ruedas de molino. Os recuerdo la variacion del voto, Q-P-U, que hubo en cada provincia:

El siguiente modelo que se me ocurre es pensar no en dos sino en tres posibles comportamientos:
- una izquierda no confluyente, u “ortodoxa”, que constituye la bolsa C
- un votante “transversal”, que constituye la bolsa A, y
- una “izquierda confluyente” que forma una tercera bolsa B, y que en las elecciones del 20D habria repartido su voto entre Podemos e IU en una razon de 1.8:1
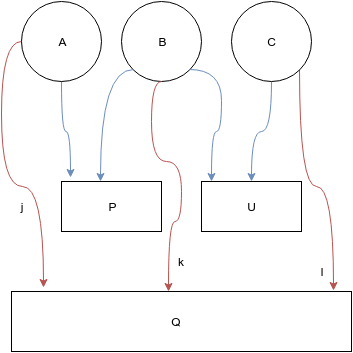
Seguramente, aunque no necesariamente, el votante confluyente habra ido a las elecciones de junio con un coeficiente k proximo a 1. En el siguiente post veré si esta idea permite un mejor ajuste a los datos.
(lo de la relacion 1.8 a 1 es por la pendiente que se ve en la grafica del post anterior. Por supuesto tambien se podria dejar ese parametro libre, pero a ver como lo medimos entonces)