Al hilo de la eleccion de presidente del gobierno, han salido dos articulos sobre teoria de juegos en la prensa: «Sanchez y la teoria de juegos«, de Fernando Garea, y «¿Por qué la teoria de juegos predice que Sanchez será presidente?», de Daniel Sarasa. Sin entrar en el fondo ni en los objetivos de cada articulo -no son inocentes, pues estan todavia las negociaciones en marcha-, queria apuntar lo complejo que resulta la nomenclatura en este area.
Un primer problema es la definicion de «equilibrio de Nash», sobre todo porque depende de si se parte de literatura evolutiva moderna, donde buscan el equilibrio de poblaciones o de literatura matematica clasica, donde buscan la solucion de juego no iterado. Y la propia definicion de estrategia cambia cuando el juego se itera.
En general, hay un punto de equilibrio de Nash cuando cada jugador individual no gana nada modificando su estrategia mientras los otros mantengan las suyas. Esta es la definicion que da Sarasa («nada que ganar si cambia») y es sutilmente diferente de la definicion de Garea («cualquiera empeora su posicion») pero es una sutilidad necesaria para que funcionen algunos teoremas de existencia. Y desde luego no coincide con el remark que añade Jose Carlos Diez al final del articulo de Garea, y que seguramente corresponde a un caso concreto de un juego determinado.
Conviene recordar que la existencia de equilibrio depende del tipo de juego. Con dos jugadores, asumiendo pagos simetricos -que no tiene por qué ser el caso- hay 14 juegos, como ya expliqué dos posts más atras.
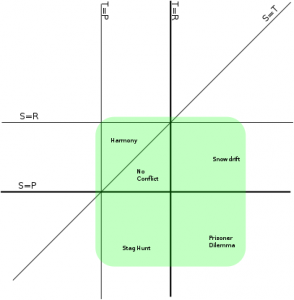
En aquel post estaba preocupado de calcular el equilibrio simetrico de Nash en los juegos con T>R y S>P, porque es el mas complicado al estar asociado a una estrategia mixta, asi que me olvide repasar los otros cuadrantes. Veamos que pasa:
Juegos con T>R, S<P: Dilema del Prisionero.
Este es el caso mas analizado. La situacion en la que ambos jugadores colaboran (jugada C, en la notacion tradicional) les permitiria cobrar R, pero si un jugador opta por jugar C el otro puede jugar D cobrando asi una cantidad T>R. Asi que la situacion en la que ambos colaboran no es un equilibrio de Nash. En cambio sí lo es la situacion en la que ambos juegan D, porque si uno esta ya en defeccion el otro no gana nada colaborando.
(Un problemilla con la nomenclatura en Dilema del Prisionero es que la jugada «colaborar con la policia» es la jugada D. Hay veces que el que lo explica se lia por utilizar «colaborar» tanto para la operacion de colaborar con el otro jugador como con la de traicionarlo.)
Juegos con T<R, S>P
Aquí la jugada C en ambos, colaborar para cobrar R, sí que es un equilibrio de Nash, porque nadie va a mejor cambiando a D; el pago de Traicion es menor que la Recompensa. Y por el contrario, la jugada (D,D), con pago P para ambos, no es equilibrio, porque cualquiera de los dos sale ganando en pasar a C: el pago de (D,C) para el que Colabora es S, que es mayor que P.
Hay cinco juegos de este tipo, y de ellos dos casos son un poco paradojicos: cuando S>R le resultaria posible a un jugador obtener mayor beneficio… ¡si convenciera al otro para que le traicionara! Naturalmente el otro jugador no lo va a hacer porque el pago de la traicion, T, es menor que el de la colaboracion, R.
Juegos con T<R, S<P
En este caso hay dos equilibrios de Nash: o bien ambos juegan C, o bien ambos juegan D. Si ambos estan jugando C no hay beneficio para un jugador en cambiar a D, porque pasaria a cobrar T que es menor que R. Y si ambos estan jugando D no hay beneficio para un jugador en pasar a C, porque el pago S es menor que P.
Asi que la paradoja en este cuadrante es que si los dos jugadores estan por algun motivo jugando ambos D, estan cobrando menos que si ambos jugaran C pero no pueden cambiar su situacion si no se ponen de acuerdo para hacerlo ambos a la vez. En un juego de una sola tirada seguramente ambos escogerian el equilibrio de recompensa dominante, pero durante una negociacion se pueden quedar atascados en el equilibrio de Nash que menos les conviene. Tambien es tipico encontrarse en este atasco evolutivamente, en juegos iterados.
Queda un cuadrante…
¿Y no hay algun juego donde el equilibrio de Nash sea (C,D) o su reciproco? Para que el jugador que esta jugando D no tenga nada que ganar, habria que pedir T > R. Y Para que el jugador que esta jugando C no tenga nada que ganar, habria que pedir S > P. Ese es el cuadrante para el que, hace dos posts, estuvimos calculando las estrategias mixtas y por su asimetricidad ignoramos la existencia de estas estrategias puras. En situacion de negociacion si que seria posible que los negociadores evolucionaran hacia un equilibrio de Nash con jugada asimetrica.
En este ultimo cuadrante si los negociadores llegan a estos equilibrios de Nash asimetricos la situacion es mas de envidietas que de paradojas. A no ser que el juego este en la linea T=S, obviamente uno de los dos cobrara mas que el otro, aunque ninguno tenga nada a ganar cambiando de estrategia. Me pregunto si es posible negociar para converger al equilbrio con estrategia mixta, que sí que es simetrico. Parece que las negociaciones deberian converger siempre a estrategias puras.
Nomenclaturas
La cuestion de la nomenclatura de los juegos puede ser especialmente importante en articulos como el de Sarasa donde parecia considerar la posibilidad de que durante una negociación cambie la matriz de pagos. Asi, no es apropiado decir que el juego es un chicken o un dilema del prisionero si precisamente la idea es ir alterando los cebos, palos y zanahorias hacia una matriz donde la solucion de equilibrio sea la que garantice consiga el objetivo lateral buscado (no convocar elecciones, o nombrar determinado presidente). El problema es que no hay mucho acuerdo acerca de los nombres mas alla del cuadrante de Dilema del Prisionero. Tambien hay que tener en cuenta que muchos articulos estudian solo el cuadrado R=1, S=0, -1<S<1, 0<T<2, que solo contiene cinco juegos distintos, pero en algunos casos sus conclusiones valen para todo el cuadrante. Para colmo, si es posible iterar el juego, la situacion se subdivide, porque entonces hay coordinaciones imprevistas, turnismos a lo Canovas y Sagasta; por ejemplo el caso donde S+T > 2R crearia nuevas paradojas.
Por ultimo hay que considerar que los teoremas de existencia aflojan enseguida cuando la matriz de pagos no es simetrica.