Un sistema con 128 nodos conectados en cuadricula, cada uno de ellos tiene 14 versos de Lope que esta dispuesto a intercambiar con sus vecinos a la busqueda de consenso.
No os preocupeis si no se entiende nada, en realidad estoy tomando la nota mental aqui en el blog para que los buscadores no me lo puntuen como irremediablemente abandonado.
Al grano. Tenemos una variable, beta, que mide la cantidad de veces que estas dispuesto a aceptar un verso de un vecino a pesar de que ello te aumenta la discrepancia con los otros tres: a mayor beta, menor disponibilidad. En un sistema fisico esta variable es la inversa de la temperatura. De aqui viene el titulo del post. La temperatura alta viene a ser la disponibilidad para admitir fluctuaciones altas, lo que solo ocurre con beta baja.
Sumamos la cantidad de disenso contando las modificaciones que habria que hacer en una coleccion de versos para producir la otra. Vamos, distancia de Levenshtein mas permutaciones. A esto se le puede llamar la energia del sistema, la cantidad que queremos acercar a cero tanto como sea posible.
Uno se da cuenta de que una beta muy baja es un desastre, porque todos vamos a ir admitiendo lo de todos sin compararlo y simplemente vamos a estar dandole vueltas y vueltas a las configuraciones. Asi que hay que elevar la beta: y en efecto a una beta muy alta, muy inflexible, cada nodo insiste siempre en admitir tan solo cambios que mejoren su coincidencia con los vecinos, la suma total de discrepancias comienza a bajar a cero a una velocidad apreciable… y luego nada, se queda colgado intentando variaciones de lo mismo. Chasco.
Lo curioso es que la velocidad de descenso no cambia suavemente con beta: a medida que la incrementamos desde un valor bajo, no se nota nada, hasta que de repente con una (in)flexibilidad critica empieza a acelerarse. Es en ese momento cuando el sistema visita mas posibilidades y por tanto se encuentra de tanto en cuando hasta con situaciones de consenso total… aunque al ser todavia la temperatura distinta de cero, de repente admite una fluctuacion, permite un poema que intercambia dos lineas de posición, y se vuelve a salir de ese minimo. Pero si seguimos aumentando beta y nos mostramos mas inflexibles para evitar fluctuaciones, no encontraremos el consenso y nos quedaremos atascados a medio camino.
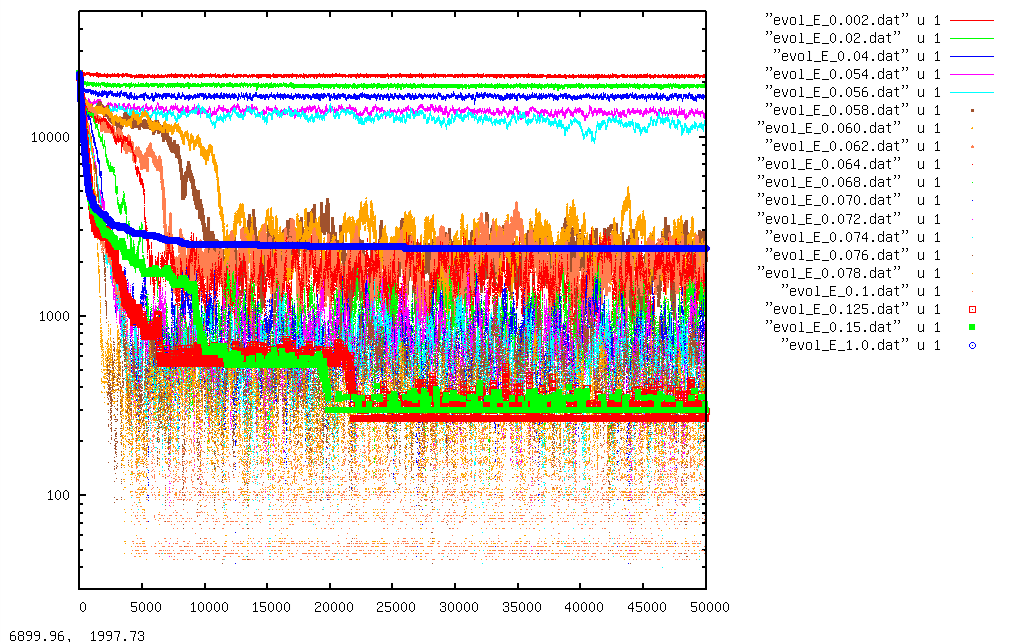
Con un poco de paciencia, todo esto se ve en la siguiente grafica:
la vertical indica la energia total, la horizontal el numero de iteraciones del sistema, y las lineas estan a diferente valor de beta. Las de beta bajo son las que permanecen practicamente horizontales: la temperatura, el ruido si quereis, evita cualquier sincronia. A mayor beta vemos esas lineas que fluctuan cada vez mas rapidamente hacia los valores bajos de energia, visitando ocasionalmente los minimos absolutos. Pero a todavia mayor beta, aparece la linea roja gruesa, y luego la verde y la azul (ahí creo que me he liado en la notación) : son estos los casos en los que más rapido parece que nos estamos poniendo de acuerdo, gracias a la inflexibilidad de no admitir una propuesta si no mejora la coincidencia con los vecinos… pero cuanto mas insistemos en esa inflexibilidad, mas nos alejamos de visitar los mejores casos de consenso global.
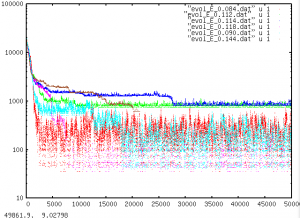
Veamos esto con mas detalle en una segunda gráfica, solo con betas por encima del valor de transición.
Los mejores casos son para beta todavía baja. Cuando se aumenta la inflexibilidad, la gran velocidad inicial se ve frustrada cada vez en mayor medida. Todavia es posible encontrar situaciones de consenso a base de echarle paciencia e iterar, y esperar que alguna solución se abrá paso de unos vecinos a otros; de hecho vemos que valores no demasiado altos de beta pueden incluso llegar a encontrar tambien una solucion optima aun despues de haber estado un buen rato atascados en las intermedias.
Por supuesto en el mundo real, y en el de las redes, el truco esta en que no solo juegas con cuatro vecinos y hay nodos que transmiten informacion a largas distancias. Pero aun con contactos locales, uno puede encontrar situaciones de “gran longitud de correlación”, jugando cerca de la llamada Temperatura de Curie.
El siguiente estudio seria añadir el “campo externo”, si se puede llamar asi a las opiniones particulares del controlador de cada nodo, y ver que soluciones se alcanzan entonces.